portals

(level : advanced)

Contents

sections	figures
Introduction	"stencil depth" sample
What is a portal ?	flat's plan - scene graph
How does it work ?	frustum reduction - culling
When is it usable ?	use in Fairy
The cycles' problem	nodes linked by several portals
Objects partially visible through portals
Case of objects straddling portals	Goldorak changing room
Objects in motion
Other properties	mirror - off/on portal
Concave or convex cells ?
Conclusion
Reference
Related pages
Appendix A : scene graph traversal's pseudo-code
Appendix B : Fairy's code excerpt

Introduction

The objects of a 3D scene are generally stored in a scene graph, a tree structure intended to organize them as a hierarchy. The most simple way to render the scene, like it is viewed from a camera, involves traversing the whole tree (= start from its root, go recursively down each branch, sub-branch, etc), and draw every object that is totally or partially visible. An object is considered 'visible' when its bounding volume (AABB, sphere or whatever) is at least partly contained in the view frustum of the camera.

This (too) simple method has two major drawbacks :

- the traversal of the whole graph takes a significant amount of time (especially since the graph probably can't entirely stay in the cache). Actually the algorithm doesn't need to explore every branch till its end : if the bounding volume of a graph's node (= volume that includes all children of this node as well as the objects it contains) is outside the view frustum, it is unnecessary to go down further as every child node is invisible.

- overdraw can be large. Ideally, each pixel of the screen should be drawn only once per rendering of the scene ; overdraw names the fact that things can be different, that some visible objects cover each other, that some completely masked faces are drawn for nothing. Overdraw is generally measured by dividing the number of pixels drawn 'for nothing' (= number of pixels drawn minus number of really visible pixels) by the number of visible pixels ; its optimal value is so zero, it is reasonable till 1 (= for each frame a pixel is drawn twice on average), and becomes problematic with bigger values. Without going down to the face level, an obvious optimization would consist in detecting the objects that are completely hidden by others, and not rendering them at all ; these occlusion tests are unfortunately quite complex (because objects have complex shapes, and can't be replaced by their bounding volumes that inevitably mask more things than they do themselves). This is why it is better to do the opposite : detect areas allowing to see 'somewhere else', for example in the neighbouring room, thanks to portals.

"stencil depth" sample from DirectX 8, showing overdraw :
- in red the pixels drawn once
- in green the pixels drawn twice
- in yellow the pixels drawn 3 times
- in blue the pixels drawn 4 times

What is a portal ?

There are two different definitions :

- for some people (and I belong to this group) a portal is a n-sided flat and convex polygon, handled in a special way at rendering time. Its goal is actually not to be drawn, but to define an area 'you' can cross to go from one place to another in the level (example : a door between two rooms, a window, a hole in a wall...). 'You' means vision in particular : if a camera in a room 'is seeing' a portal of this room, this means it can also see what is 'on the other side' of the portal. A portal establishes a link between two graph nodes, that don't necessarily have any other relationship.

- other people consider those polygons divide the scene in small parts, and they call these pieces portals. So their 'portals' correspond to my 'rooms', they are no more polygons but volumes, they can be convex or concave depending on the pursued aim (a concave volume can always be subdivided into several all convex volumes). I will precise this concept of convex / concave volumes later because it's very important, for the moment let's come back to our definition of the portal : in this whole document it means my n-sided flat and convex polygon, but be aware that in other texts it can represent an elementary volume of the scene (or 'cell').

Let's take the example of a house : the graph's root represents this whole house, each node under the root is a room, each room contains furniture, in pieces of furniture there are objects, etc. This is the same thing in the demo #4 of Fairy : the 'first level' nodes (if the root is the 0-level) each represent a room or a corridor, their children are the objects placed in this room (for example in the central room : 4 'wall' objects, 1 ceiling, 1 floor, 1 staircase, 1 fountain, 2 particle systems, 1 light - the doors' case is a bit special because they are at the borderline between two rooms). Portals are placed on each 'hole' allowing to go to the neighbouring room or corridor, their shapes fit exactly those of the passages (simple rectangles).

Note : because portals are polygons, they could be stored with 'normal' faces, a flag indicating they have to be treated differently ; however it is simpler to keep them in a separate list, especially as they can contain additional information as we'll see later.

example : rough plan of my flat (inaccurate scale)

A : bedroom 1 - B : bedroom 2 - C : bathroom - D : corridor - E : toilets - F : entrance - G : kitchen - H : living room - I : balcony
red = door - green = window - red+green = French window

corresponding scene graph (one possibility among others), stopped at level 1

in red : portals (numbered in blue) linking the rooms

How does it work ?

The rendering of the scene doesn't start at the graph's root, but with the node that contains the wanted camera ; because the camera is in this room, this one is necessarily visible, and we begin by drawing it as well as its subnodes (= what it contains), restricting ourselves like previously to the 'visible' objects (= in the view frustum). If among these objects or the subnodes' ones there is no visible portal, then the rendering is finished ; if on the contrary a portal is visible, the node it leads to is visited, and so on recursively.

Optimization : when a portal is visible, it means the room it leads to is visible, but only partially, because the camera can only see this room through the portal (and not through the walls that are on each side of the door, for example). The view frustum of the camera can therefore be modified and reduced to only look through the door's opening, and this has a double advantage : on one hand less objects of the neighbouring room are going to be detected as visible and drawn for nothing (this will reduce overdraw), on the other hand few other portals will have the opportunity to be visible, and the graph traversal is going to stop quickly. That's where the true advantage of the method lies.

view frustum reduction when crossing the portals

in blue : what the camera is seeing - in grey : some 'invisible' objects - in yellow : some 'visible' objects

Let's enter the details of the view frustum reduction. If a visible portal was always completely inside the view frustum, it would suffice to replace this one by the new smaller view volume. This new volume is defined in the following way : each edge (= 2 consecutive points) of the portal's polygon form a plane with the camera's position (= 3rd point), and the n planes together delimit the volume. This is true provided that the 3 points used to define each plane are distinct, which implies that : - the polygon is not degenerate, - the camera is not exactly on one of the points of the polygon, two easy to satisfy conditions (in a game the camera has a bounding volume, and can't come closer than a certain distance to the walls or the colliding objects, for example 50 cm).

But a portal can be only partially visible (on the above figure : the portal 4 between the entrance and the corridor), which means that the new volume projects beyond the view frustum, and is not optimal (NB: a more vicious problem : the view frustum is reduced for the visibility tests, but it's still the original frustum that is used to project the objects on the screen, which means that some objects could extand beyond the screen, the clipping not being performed correctly anymore. A software renderer will crash immediately ; with hardware accelerated graphics cards the result is undefined if you use a flag to tell them not to clip, when you have found that the processed object is entirely inside the view volume). The optimal volume is the intersection of the initial frustum with the new volume, and it is not even necessary to calculate this intersection (which simplifies the algorithm).

I suppose you already know how to establish that an object is in the view frustum of a camera : actually one looks if it's not outside the frustum in an obvious way, by checking if it's not completely 'outside' with respect to one of the frustum's planes. This method is not perfect (some objects will be considered visible when they are not), but is simple, fast, and however very efficient (it excludes a big percentage of invisible objects, and inevitably keeps all the visible ones). It can be used with any convex volume defined by planes, and is not reserved for frustums ;) This explains why the portal needs to be a convex polygon : this property ensures the fact that the volume that is going to be created from the portal and the camera position is also convex.

finding objects that are in the view frustum (= "culling")

in blue : the view frustum
in grey : some 'invisible' objects (outside the frustum with respect to the left 3 or the right 4 planes)
in yellow : a 'visible' object
in orange : an object supposed to be visible (it's not outside the frustum with respect to the far plane 2, nor the right plane 4), wrongly

The intersection of 2 convex volumes is a convex volume (or an empty one, which would mean the portal is invisible), but I've said we are not going to calculate it : an object is inside this intersection if it's inside each of the 2 volumes. The initial view frustum consists of 6 planes (top/bottom/left/right/near/far) ; when a portal is crossed, the planes it forms with the camera are calculated, and added to the view volume. The objects processed next are tested against all these planes, until the recursive function comes back to the start node, and the added planes are poped. As soon as an object is outside the volume with respect to one of the planes, the tests stop (it is invisible) ; however you have to avoid the number of planes to increase too fast or the tests take longer, which leads to the following rule : a portal must stay a simple shape, without 'too many' edges. If a hole in a wall (for example) has a complex shape, the corresponding portal is simply a convex polygon that includes this shape, in most cases a rectangle (or a lozenge, or a parallelogram) is enough.

When is it usable ?

I've talked a lot about 'rooms', doors, walls, etc. Portals are in fact particularly well suited for interiors, because they avoid drawing objects or rooms hidden by walls. Outside, vision is a lot more free, less limited by low distance obstacles, and occlusion algorithms (test to find 'who hides who') are more appropriate.

The demo #4 of Fairy is a good example of a case where the use of portals is very beneficial : each room contains objects with many polygons, but you can never see more than two rooms at the same time. The more partitioned the world is, the more objects (with many faces) there are, the more interesting it is. Imagine I extend my test level, and I multiply the number of rooms by 10, each one containing on average as many faces as the actual rooms ; if I can manage to keep the 'no more than 2 visible rooms at the same time' rule, calculations will stay quite identical and the framerate will be maintained to its current value.

use of portals in Fairy

main room

with the portals

without the portals

the difference is notable behind Lara : without the portals, the cats' room is visible and drawn, despite it's entirely masked by three walls (click to enlarge the pictures).

The cycles' problem

The principle of rendering with portals has nothing complex, but a problem immediately appears : if a portal P links two nodes N0 and N1, and if P is visible when N0 is drawn, then N1 is going to be visited, P is going to be visible again, and we're going to come back to N0 ! The recursive graph traversal function will enter an infinite loop, and end with a 'stack overflow'. In Fairy the problem doesn't arise because the portals are crossed only when they face the camera, that is to say if the camera is on the side of the portal's plane pointed to by its normal (like every polygon, a portal has got a normal). In my example, if the camera is attached to the node N0 and can cross the portal P (= it is in the view frustum, and its normal points to the camera), when the node N1 is drawn it is impossible to re-cross P in the other direction because for N1 the normal is reversed. To be perfectly precise, it is laborious to manage a face having two opposite normals, and there is not 1 but 2 portals in Fairy to link two rooms to each other : P0 which allows to go from N0 to N1, and P1 that goes in the N1->N0 direction. The two polygons are identical, but have opposite normals (each one points the interior of the node that is the origin of the portal). This system avoids the case of a simple return between two nodes, but doesn't protect against more complex cycles like N0->N1->N2->N0, or even N0->N1->N0 if the ways there and back don't use the same portal (two rooms can communicate by several doors, or windows).

Cycles only appear if the rooms are concave, and have quite bad chosen shapes, and it would always be possible to avoid them automatically or by hand by splitting the concave rooms into convex pieces of room. There is another solution : flag the nodes that have already been drawn, and not visit them a second time. This solution doesn't work : if N0 and N1 communicate by two doors P0 and P1, from N0 one can see objects of N1 through P1 that are not visible through P0, and have therefore not been drawn when N1 was first visited (supposing the algorithm crosses P0 before P1). So, these are in fact the objects that need to be flagged : whether it's visible through a portal or another, an object has only one position in the scene, and will be drawn at the same place of the screen for a given camera.

two nodes N0 and N1 linked by 3 portals

in blue : the view frustum
in orange : 2 'visible' objects in N1
A is visible through the left portal, B is visible through the two other portals (but only needs to be drawn once)

To avoid having to reinitialize the 'already drawn object' flags before rendering each frame, a 32 bits counter (corresponding for example to the frame number) is used : when an object is visible, the value of the counter is compared to the current value, if they're different it means that the object has not been drawn for this frame, so it is rendered and its counter is being updated. If we have a match, we go to the next object.

Note : an object can be drawn several times during the same frame, if it's seen and at the same time reflected by a mirror. In the case of a flat mirror (the only case we can deal with in real time), a symmetrical object about the mirror is not created, instead it is the camera that is reflected (this is a lot faster, and the result is the same, cf your classes of optics). To allow another rendering of the object, it is possible to play with the frame counter, and increment it when the mirror is 'crossed' (the mirror is a special portal : its source and destination nodes are the same, and it modifies the camera that crosses it).

Another way to proceed is to change the rule 'an object can't be drawn more than once in a frame', which is false with mirrors, to : 'an object can only be drawn once per frame from a given camera'. When a mirror is detected, a new camera corresponding to the reflection of the current one is created, and this camera can draw every object that is in its view frustum in its turn. This implies that a list of already drawn 3D objects is kept in the camera object, and each object is compared to this list before being rendered (and added to the list). These comparisons inevitably take a little more time than the counter system, but this is the method I'm using at that time in Fairy (my list is in fact an STL 'set').

If two mirrors are facing each other, and the camera's view direction is aligned with their normals, it's going to be reflected over and over by one and then the other mirror (in a kind of infinite ping pong). In this case, one solution is to introduce a counter in the portal that tells how many times it has been crossed, and limit this value to two for example. You then have to remember to reset these counters to zero at the beginning of each frame (this is faster than in the case of objects, if a static list of every portal in memory is kept in the CPortal class).

Objects partially visible through portals

When an object is only partially visible through the polygon of a portal, one could be tempted to clip the piece or pieces that extend beyond the polygon. This is not a good idea : clipping is a quite complex task , that creates faces that can have more vertices than the original faces (ex : the clipping of a triangle gives a triangle or a quad), TnL cards don't like their vertex buffers to be modified, and moreover this is completely useless. These pieces are either hidden by the wall (or another object) that surrounds the portal, or visible through other portals and will in this case need to be drawn. The rendering 'for nothing' of certain faces of the object is not very expensive (less than removing these faces and splitting others), if the object has a number of faces that makes this problem worrying then it means it is a bad mesh : it must be split into several sub-objects.

There are two solutions for the wall (for example) to mask the object correctly : draw this wall after the object (that is to say begin by drawing what's behind the portal, and render the objects of the room it belongs to only after), or let the z-buffer do the job. This second option is of course the most interesting one, because it allows to draw the objects of each room in any order, and not only to render the rooms in any order.

To not clip the objects by the planes of the portals (they however need to be clipped by the planes of the camera's view frustum, but TnL cards or the API take care of that) increases overdraw a little, in very reasonable proportions. If you absolutely want to avoid this extra overdraw, it is possible to get rid of it by using user clipping planes. This is a solution I advise you against in the actual state of available hardware : with a non TnL card it is the API that is going to do the clipping in an unefficient way, with a TnL card the number of user clipping planes that can be used at the same time is very small (generally 4 or 6) and don't forget that the routine for graph's traversal is recursive and pushes 4 planes per crossed portal on average, on some consoles (Xbox) user clipping planes don't really exist and are simulated by the card thanks to a trick.

Sure, user clipping planes would have the advantage to not need to perform visibility tests against the portals' planes anymore, because in addition to clip partially visible objects, they would totally eliminate those that are not. But this solution seems too expensive to me, because it means that all objects are sent to the 3D card, even those that can be quickly removed with some simple tests of their bounding volumes.

Case of objects straddling portals

Goldorak changing room
(see the message "CHR PORTAL COLL : TRUE" - click to enlarge)

What happens when an object is at the same time a little on both sides of a portal ? Imagine for example a column in a greek temple, fallen across a door (I've made this test), or more probably a moving object passing through the door to go from one room to another one (NB : moving objects and the crossing of portals will be explained in the next section, let's suppose for the moment that the object is stationary). It has to be attached to the two rooms linked by the portal, as it can be visible as soon as the camera is 'visiting' one of these rooms, even if the portal is outside the view frustum. Attaching an object to two nodes of the scene graph however creates several difficulties :

- if each room has its own 3D local space (position and orientation with respect to its parent node), that is to say if all objects are not positioned in a single space (the scene's one), attaching an object to two nodes means giving it two different positions and orientations. Though they correspond in fact to a unique positioning in the scene, this is generally not desirable. For example, when the object is moved the two positions need to be updated ; and what is to be done when one of its parent nodes (and not the other) is moved : move the object to follow one parent, or let it immobile with the other ?

- if the nodes the object is attached to are both visible, the object could be drawn twice (unless it is flagged as explained in the section about cycles).

- the problem is not limited to two nodes : an objet can very well straddle more 'cells' of the world, they don't necessarily represent rooms like in Fairy and can be very small, particularly if the portals are not placed in the level by hand but by an automatic splitting algorithm.

Another possibility is imaginable : to split the objects straddling portals into several parts. It is perhaps appealing in the case of static objects, but not at all when it is about deformable or moving objects, when precalculating the results is inconceivable.

So I've chosen another solution. Each object can only have one parent (or zero if it's not attached to the graph), which simplifies the positioning problems (NB : this doesn't exclude the sharing of data = reuse of the same object in several places of the level, this is simply not the object (the mesh) that is shared, but the data it contains, its faces or vertices). An object straddling one or several portals is arbitrarily attached to one of the concerned nodes (for example the one that contains the bigger part of the object. In Fairy, each object being defined in its own space ('model space'), it is attached to the node that contains the origin of this space). In order to record the fact that it is also present in other parts of the scene, and can be visible even if its parent is not, it is attached to the other nodes as a 'visitor' (it is a term I have invented for the occasion). In addition to its list of objects, subnodes, and portals, each node so has a list of visitors. They are processed like 'normal' objects with respect to rendering and collisions, but take their position / orientation from their single parent. They keep a pointer to this parent, like all objects do. They are only drawn once per frame (unless there are mirrors) thanks to the method explained above (list of objects rendered from a given camera).

An example of 'visitors' in the demo #4 : the doors of the central room, which are attached to the corridors but also to this room. And of course the character, when he/she goes from one place to another.

Objects in motion

At a given time, each object in motion (character, camera, etc) is attached to a node, and is in one or more cells (= rooms) separated by portals. What happens when such an object moves between 2 frames ?

The wanted move must first be validated : collision tests are performed with the other objects of the node the object is attached to (including the 'visitors'), with the portals of this node, and then with the objects and portals of the neighbouring nodes if the object is actually straddling one or more portals, and so on recursively. If there is a collision with an object, the move is either discarded, or modified (bounce on a wall, etc) until it's valid.

When the move is accepted, if the object isn't crossing any portal when doing this move, there is nothing special to do. On the contrary if the object is changing node (in Fairy : if the origin of the object is going to the other side of the portal), for each crossed portal you need to : detach the object from its current node, attach it to the node the portal leads to, and calculate the new local position and orientation if each node has its own space (this is the case in Fairy).

After the move, if the object is colliding some portals, don't forget to attach it as a 'visitor' to the concerned neighbouring nodes. The scene can then be rendered, everything is ready.

NB : I'm not going to give details here about how the collision tests are done, this is the subject of another article. It is very important they work well, if an object crosses a portal without noticing it (= without any change of the parent node) the whole method falls through.

Other properties

A portal can have other properties than the polygon and the source and destination nodes that define it. For example, it can contain a 3D transform (translation + rotation + scale...), that modifies the characteristics of the camera that crosses it, like its position and orientation. Two classical uses : mirrors (the transformation is a symmetry with respect to the portal's plane, z = -z in Fairy), and teleporters or spy cameras (what is drawn behind the portal corresponds to another part of the scene). These effects are obtained almost for free once the scene graph's traversal using portals has been implemented.

a classical use of portals : the mirror

The geometry under the floor (rooms, Lara, fountain, particles) doesn't really exist, this is the one that is seen by the reflected camera.

A portal can also have a volume bounding its polygon if this one has many sides, in order to find more quickly if it's in the view frustum of the camera ; however I recall it is desirable to have simple polygons, so that not too many planes are pushed during the reduction of the view volume.

The portals of Fairy have an on/off flag, that tells for each of them if it's enabled or disabled. A disabled portal will not be crossed. This is useful when the engine or the game knows that what's behind the portal is masked and so invisible. This is shown in the demo #4 : when the doors of the central room are completely closed, the corresponding portals are disabled, and the corridors or the central room (depending on what side you are) are not drawn. You can see it in wireframe : open the doors, go to wireframe mode (W key), step back to let the doors close again, and watch what happens behind them.

disabled / enabled portal

closed doors

opening doors

(click to enlarge the pictures)

Some portals can be crossed by objects (those that are useful for visibility tests, or teleporters), other can't (mirrors, spy cameras). A flag can be added to store this feature, but it is generally useless : when a portal is 'blocking', there is often a mesh covering the same place, and that is enough to prevent moving objects from going through.

Concave or convex cells ?

It is now time to come back to an important point mentioned earlier : do the portals have to split the scene into concave or convex cells ? If you choose the concave cells, all shapes are allowed without restriction, which simplifies the creation of the scene ; if you choose the convex cells, the concave ones need to be cut in several convex bits, which is always possible. The decision depends on the advantages and drawbacks of each solution, and the importance you attach to these advantages and drawbacks.

Advantages of convex cells :
- they guarantee there will not be any overdraw at all, which was our initial objective. This also means that the visible objects or pieces of objects can be rendered in any order, and without the help of the z-buffer, provided those that are partially visible are clipped (cf "Objects partially visible through portals" above)
- intersection and collision tests are simpler with convex objects than with concave (= of any shape) ones, having a world completely made of convex cells is very useful in this field
- from any point of a convex object you can go to another point of this object without being outside of it (this is the definition of convexity) ; if a character has to go from a place A to a place B, it is enough to find a path between these two places only made of empty cells : inside each of those cells the character will be able to move without encountering any fixed obstacle (however it can bump into other characters or moving objects). This simplifies the pathfinding for NPCs (Non Playable Characters).

Drawbacks of convex cells :
- the splitting of the scene into convex cells can require a very big number of portals (imagine a sphere in the center of a room and you've got the most disastrous case because each face of the sphere is going to create several portals). This is perhaps the only drawback but it's very serious, as it leads to the following points :
- the splitting can take a lot of time ; it's going to be a pre-calculation phase (like for a BSP). The world will be fixed, creating or modifying portals at runtime can result in a lot of processing (in order to keep the convexity property)
- the scene will take more memory, and more place on the hard drive or CD ROM
- portals being more numerous, and the graph being bigger, the scene's traversal will take longer
- cells being smaller on average, the moving objects will be in more cells at the same time

Advantages of concave cells :
- portals can be placed by hand by the artist or the designer, in a more intelligent way than with an automatic splitter
- cells reflect the architecture of the level, they correspond to logical entities (rooms, corridors, stairs...)
- the graph traversal is fast, in return for a bit of overdraw
- partially visible objects don't have to be clipped (with a bit of extra overdraw too)
- it is easy to modify the level in real time, for example to create a hole in a wall (you only need to know which node is on the other side of the wall)

Drawbacks of concave cells :
- overdraw is not reduced to zero
- intersection and collision tests are more complex
- the architecture of the scene doesn't give any information for the pathfinding

The choice is up to you. In Fairy cells are concave, because I'm not a big fan of long preprocessing stages, and 3D worlds becoming more and more huge and detailed in games, it seems to me that it's bad (= too long and memory expensive) to split them into tiny pieces. Concave cells allow to strongly reduce overdraw (and so to speed up rendering), without complicating other stages of the 3D pipeline a lot.

Conclusion

Portals are generally blaimed for two things : they generate a lot of tests (of visibility), and a lot of clipping (of partially visible objects). We've seen that this is not true in the case of concave cells, because the number of portals remains limited, and objects don't have to be clipped.

It is not really possible to compare portals with BSP (some of you certainly ask themselves this question) : their goals are not the same. The BSP's one is to get a perfect order to draw the objects from front to back or back to front whatever the camera's position is in the world (but everything is rendered, overdraw is avoided differently), the one of portals with convex cells is to suppress overdraw, the one of portals with concave cells is to limit strongly and quickly the number of visible objects with the addition of some tests and extra data (that are very light compared to the two other methods).

Reference

a very detailed tutorial (17 issues !) on Flipcode

Download articles
Download Fairy demos

Appendix A : scene graph traversal's pseudo-code

note : it is in fact the code presented in appendix B, described and summarized in a few words ('details' are omitted)

simple traversal without portal

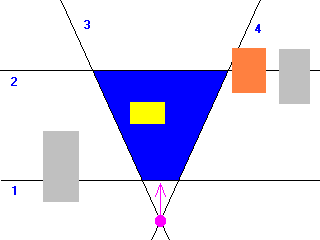
node = graph's root
node->SimpleTraversal(camera)

node::SimpleTraversal(camera)           // recursive function
{
  node->Draw(camera)                    // draw the content of the node (= attached objects)

  for each child of the node            // = each subnode
    child->SimpleTraversal(camera)

  for each 'visitor'                    // = subnode attached to another node,
                                        //   but that extends (is visible) in this one
    visitor->SimpleTraversal(camera)
}

node::Draw(camera)
{
  if there is at least one object in the node : activate the lights that affect the node

  for each object of the node
    if the object is a visitor and has already been drawn : skip it
    if the object is invisible : skip it
    if the object's bounding volume is outside the view frustim : skip the object

    object->Draw
    if the object is a visitor : add it to the list of already drawn objects in the camera
}

traversal with portals

node = room the camera is in
node->PortalsTraversal(camera)

node::PortalsTraversal(camera)
{
  reinitialize the view frustum         // = suppress planes added by the portals
  node->PortalsRecursiveTraversal(camera)
}

node::PortalsRecursiveTraversal(camera)
{
  for each portal attached to the node
    dest = corresponding destination portal
    destnode = destination portal's node

    if the portal is disabled, skip it
    if the portal's bounding volume is outside the view frustum, skip the portal
    if the portal's bounding volume is outside the reduced frustum, skip the portal

    transform the camera's position to the portal's space
    if the camera is not facing the portal (= is not on the side pointed by its normal), skip the portal

    transform the portal's bounding volume (an AABB) to the camera's space
    calculate the equations of the planes formed by the camera and the edges of the transformed volume
    add these planes to the camera's view frustum

    if the portal has a 3D transformation (mirror, teleport...)
      calculate the camera's transformed position and orientation 
      create a new camera with these parameters
      copy the planes of the current camera to the new one

      destnode->PortalsRecursiveTraversal(new camera)

    else
      destnode->PortalsRecursiceTraversal(camera)

    suppress the planes added to the camera by this portal

  //

  node->Draw(camera)                    // function described above

  //

  for each child of the node            // = each subnode
    child->PortalsRecursiveTraversal(camera)


  for each 'visitor'                    // = subnode attached to another node
                                        //   but that extends (is visible) in this one
    visitor->PortalsRecursiveTraversal(camera)
}

Appendix B : Fairy's code excerpt

I am sure some of you want to see some 'real' code, even if it's only a few functions, given without additional explanations. The first two correspond to the 'simple' traversal, the next two to the traversal using portals.

If you look a little closer you'll see I use STL for the nodes / portals / visitors lists. This code is only an example, subject to future modifications, some parts like the writing in the stencil buffer are not used anymore at the time being (NB : the stencil is another way to clip objects partially visible through portals).

If you decide one day to write your own portals' system, I advise you not to start from this code, but only from the above article or any other source of information on the subject. Algorithms are important, any particular implementation of somebody or somebody else is not. To your keyboards ;)

/**********************************************************************************************************************/
/*                                                GRAPH TRAVERSAL                                                     */
/**********************************************************************************************************************/

/************************************************ dwSimpleTraversal ***************************************************/
// traverse graph to render visible objects - init                                                                      
// 22/04/01, M                                                                                                          
// in : current camera,current frame number                                                                             
// out: number of nodes traversed                                                                                       
// rem: simply follow the tree, no portals                                                                              
/**********************************************************************************************************************/

DWORD CGraphNode::dwSimpleTraversal(const CCamera* lpCamera,const DWORD dwFrame)
  {
  DWORD dwNodes = 0;
  vSimpleTraversal(lpCamera,dwFrame,&dwNodes);
  return dwNodes;
  }

/************************************************ vSimpleTraversal ****************************************************/
// traverse node & children (recursively)                                                                               
// 22/04/01, M                                                                                                          
// in : current camera,current frame number,node counter address                                                        
// out:                                                                                                                 
// rem: simply follow the tree, no portals                                                                              
/**********************************************************************************************************************/

void CGraphNode::vSimpleTraversal(const CCamera* lpCamera,const DWORD dwFrame,DWORD* lpdwNodes)
  {
  CCamera* lpCam   = const_cast<CCamera*>(lpCamera);
//  if(m_dwTraversalSee == dwFrame) return;                   // already traversed; avoid infinite loop
  m_dwTraversalSee = dwFrame;
  (*lpdwNodes)++;

  // traverse node

  hrDraw(lpCamera);

  // traverse children

  listNodeIterator itChild = m_listChildren.begin();        // DON'T use lpGetFirstChild because of shared iterator !

  while(itChild != m_listChildren.end())
    {
    CGraphNode* lpChild  = *itChild;
    CBVbase*    lpBVNode = lpChild->lpGetBoundingVol();
    CMat4x4     m4Node2World;

    if(lpBVNode)
      {
      if(lpChild->boGetWorldMatrix(&m4Node2World))
        lpBVNode->vSetTrf2World(&m4Node2World);
      }

    lpChild->vSimpleTraversal(lpCamera,dwFrame,lpdwNodes);
    itChild++;
    }

  // traverse visitors

  setNodeIterator itVisitor = m_setVisitors.begin();

  while(itVisitor != m_setVisitors.end())
    {
    CGraphNode* lpVisitor = *itVisitor;
    CBVbase*    lpBVNode  = lpVisitor->lpGetBoundingVol();
    CMat4x4     m4Node2World;

    if(lpBVNode)
      {
      if(lpVisitor->boGetWorldMatrix(&m4Node2World))
        lpBVNode->vSetTrf2World(&m4Node2World);
      }

    lpVisitor->vSimpleTraversal(lpCamera,dwFrame,lpdwNodes);
    itVisitor++;
    }
  }

/************************************************ dwTraversal *********************************************************/
// traverse graph to render visible objects - init                                                                      
// 27/04/00, M                                                                                                          
// in : current camera,current frame number                                                                             
// out: number of nodes traversed                                                                                       
/**********************************************************************************************************************/

DWORD CGraphNode::dwTraversal(const CCamera* lpCamera,const DWORD dwFrame)
  {
  lpCamera->lpGetBVPlanes()->vSetTrf2World(lpCamera->lpm4Get2WorldMatrix());
  lpCamera->lpGetBVPlanes()->vRemoveAll();                  // planes are in camera space

  DWORD dwNodes = 0;
  vTraversal(lpCamera,dwFrame,&dwNodes);
  return dwNodes;
  }

/************************************************ vTraversal **********************************************************/
// traverse node & children (recursively)                                                                               
// 27/04/00, M                                                                                                          
// in : current camera,current frame number,node counter address                                                        
// out:                                                                                                                 
/**********************************************************************************************************************/

void CGraphNode::vTraversal(const CCamera* lpCamera,const DWORD dwFrame,DWORD* lpdwNodes)
  {
  CCamera* lpCam   = const_cast<CCamera*>(lpCamera);
//  if(m_dwTraversalSee == dwFrame) return;                   // already traversed; avoid infinite loop
  m_dwTraversalSee = dwFrame;
  (*lpdwNodes)++;

  // traverse portals

  listPortalIterator itPortal = m_listPortals.begin();        // DON'T use lpGetFirstPortal because of shared iterator !

  while(itPortal != m_listPortals.end())
    {
    CGraphPortal* lpPortal   = *itPortal;
    CGraphPortal* lpGoal     = lpPortal->lpGetGoal();
    if(!lpGoal)
      {
      if(lpPortal->dwGetType() == CGraphPortal::_MIRROR_)
        lpGoal = lpPortal;
      else
        {
        itPortal++;
        continue;
        }
      }

    CGraphNode  * lpNode     = lpGoal  ->lpGetParentNode();
    CBVbase     * lpBVPortal = lpPortal->lpGetBoundingVol();

    // set portal->world trf

    CMat4x4 m4Portal2World;
    if(lpBVPortal && lpPortal->boGetWorldMatrix(&m4Portal2World))
      lpBVPortal->vSetTrf2World(&m4Portal2World);

    // transform camera position to portal repere

    CVect3D  v3CamWorldPos;
    CVect3D  v3CamPortalPos;

    // portal in camera frustum ?

    if(lpPortal->boIsEnabled() && lpCam->dwIsInFrustum(lpPortal))
      {
      // test against previous portals
      // rem: planes are in camera space (to be node-independent)

      CBVPlanes* lpPlanes = lpCam->lpGetBVPlanes();

      if(lpBVPortal && (lpPlanes->hrIntersection(lpBVPortal) != CBVbase::_OUTSIDE_))
        {
        if(lpCam->boGetNodeWorldPos(&v3CamWorldPos) && lpPortal->boTransformToRepere(&v3CamPortalPos,v3CamWorldPos))
          {
          if(v3CamPortalPos[_Z_] > 0.f)
            {                                               // portal facing the camera
            // test : draw portal (mesh) to stencil

            if(m_lpRenderer->boAllowStencil())
              {
              m_lpRenderer->vSetStencilWrite();
              hrDraw(lpCamera);
              m_lpRenderer->vSetStencilTest();
              }

            // push planes

            DWORD dwPlaneNum[4];

            if(lpBVPortal && m_boPortalCulling)
              {
              CBVAABB* lpPortalAABB = reinterpret_cast<CBVAABB*>(lpBVPortal);
              CVect3D  v3Min,v3Max;
              lpPortalAABB->vGet(&v3Min,&v3Max);

              CVect3D  v3Corner[4];                         // build corners (portal seen front => X to the left)
              v3Corner[0].vSet(v3Max[_X_],v3Min[_Y_],0.f);
              v3Corner[1].vSet(v3Max[_X_],v3Max[_Y_],0.f);
              v3Corner[2].vSet(v3Min[_X_],v3Max[_Y_],0.f);
              v3Corner[3].vSet(v3Min[_X_],v3Min[_Y_],0.f);

//              CMat4x4  m4World2Cam;
//              lpCam->boGetNodeWorldMatrixI(&m4World2Cam);
//              CMat4x4  m4Portal2Cam = m4World2Cam*m4Portal2World;
              CMat4x4  m4Portal2Cam = (*lpCam->lpm4Get2CamMatrix()) * m4Portal2World;

              CVect3D  v3Proj[5];                           // trf to camera space
              v3Proj[0].vSet(m4Portal2Cam*v3Corner[0],_W_);
              v3Proj[1].vSet(m4Portal2Cam*v3Corner[1],_W_);
              v3Proj[2].vSet(m4Portal2Cam*v3Corner[2],_W_);
              v3Proj[3].vSet(m4Portal2Cam*v3Corner[3],_W_);
              v3Proj[4].vSet(v3Proj[0]);

              // build plane eq

              for(DWORD dwPlane = 0; dwPlane < 4; dwPlane++)
                {
                CVect3D v3_01(v3Proj[dwPlane+1]-v3Proj[dwPlane]);
                CVect3D v3N  (v3Proj[dwPlane]  ^v3_01);
                if(lpCam->boIsLeftHanded()) v3N = -v3N;
                CVect4D v4Eq (v3N,0.f);

                dwPlaneNum[dwPlane] = lpPlanes->dwAddPlane(v4Eq);
                }
              }

            // portal changes camera parameters

            if(lpPortal->boUseSpecial())
              {
              // trf to portal space

              CMat4x4 m4I;
              lpPortal->boGetWorldMatrixI(&m4I);
              m4I[_X_][_W_] = m4I[_Y_][_W_] = m4I[_Z_][_W_] = 0.f;

              CVect3D v3CamWorldDir,v3CamWorldUp;
              lpCam->boGetNodeWorldDir(&v3CamWorldDir);
              lpCam->boGetNodeWorldUp (&v3CamWorldUp);

              CVect3D v3CamPortalDir(m4I*v3CamWorldDir,_W_);
              CVect3D v3CamPortalUp (m4I*v3CamWorldUp ,_W_);

              // apply special trf (no translation)

              CMat4x4* lpm4Trf = lpPortal->lpm4GetSpecialTrf();
              v3CamPortalDir.vSet((*lpm4Trf)*v3CamPortalDir,_W_);
              v3CamPortalUp .vSet((*lpm4Trf)*v3CamPortalUp ,_W_);
              v3CamPortalPos.vSet((*lpm4Trf)*v3CamPortalPos,_W_);

              // back to world space

              CMat4x4 m4M;
              lpPortal->boGetWorldMatrix(&m4M);
              m4M[_X_][_W_] = m4M[_Y_][_W_] = m4M[_Z_][_W_] = 0.f;

              v3CamWorldDir.vSet(m4M*v3CamPortalDir,_W_);
              v3CamWorldUp .vSet(m4M*v3CamPortalUp ,_W_);
              lpPortal->boTransformToWorld(&v3CamWorldPos,v3CamPortalPos);

              // new camera

              CGraphNode nodNew;
              CCamera    camNew(*lpCam);
              nodNew.vSetAutoDelete(false);                 // local vars can't delete themselves
              camNew.vSetAutoDelete(false);

              nodNew.boAttachObject (&camNew);
              nodNew.vSetPosition   (v3CamWorldPos);
              nodNew.vSetOrientation(v3CamWorldDir,v3CamWorldUp);

              camNew.vSetLeftHanded(!lpCam->boIsLeftHanded());
              camNew.boCalcTrfMatrix();

              // copy BV planes

              DWORD      dwPlanes    = lpPlanes->dwGetNbPlanes();
              CBVPlanes* lpNewPlanes = camNew.lpGetBVPlanes();
//              CMat4x4    m4Cam2World;
//              camNew.boGetNodeWorldMatrix(&m4Cam2World);
//              lpNewPlanes->vSetTrf2World (&m4Cam2World);
              lpNewPlanes->vSetTrf2World(camNew.lpm4Get2WorldMatrix());

              for(DWORD dwPlane = 0; dwPlane < dwPlanes; dwPlane++)
                {
                lpNewPlanes->dwAddPlane(lpPlanes->v4GetPlane(dwPlane,NULL));
                }

              // recurse

              m_lpRenderer->boBegin3D(&camNew);             // new cam->world trf

              m_lpRenderer->vSetCullMode(camNew.boIsLeftHanded());
              lpNode->vTraversal(&camNew,dwFrame,lpdwNodes);
              m_lpRenderer->vSetCullMode(!camNew.boIsLeftHanded());

              m_lpRenderer->boBegin3D(lpCam);               // restore
              nodNew.boDetachObject(&camNew);               // don't forget that, the camera could be destroyed before the node
              }

            // same camera

            else
              {
              lpNode->vTraversal(lpCamera,dwFrame,lpdwNodes);
              }

            // pop planes

            if(lpBVPortal && m_boPortalCulling)
              {
              lpPlanes->boRemovePlane(dwPlaneNum[0]);
              lpPlanes->boRemovePlane(dwPlaneNum[1]);
              lpPlanes->boRemovePlane(dwPlaneNum[2]);
              lpPlanes->boRemovePlane(dwPlaneNum[3]);
              }

            // disable stencil

            if(m_lpRenderer->boAllowStencil())
              {
              m_lpRenderer->vSetStencilOff();
              }
            }
          }
        }
      }

    itPortal++;
    }

  // traverse node

  hrDraw(lpCamera);

  // traverse children

  listNodeIterator itChild = m_listChildren.begin();        // DON'T use lpGetFirstChild because of shared iterator !

  while(itChild != m_listChildren.end())
    {
    CGraphNode* lpChild  = *itChild;
    CBVPlanes*  lpPlanes = lpCam  ->lpGetBVPlanes();
    CBVbase*    lpBVNode = lpChild->lpGetBoundingVol();
    CMat4x4     m4Node2World;

    if(lpBVNode)
      {
      if(lpChild->boGetWorldMatrix(&m4Node2World))
        lpBVNode->vSetTrf2World(&m4Node2World);
      }

//!!!    if(!lpBVNode || (lpPlanes->hrIntersection(lpBVNode) != CBVbase::_OUTSIDE_))
      {
      lpChild->vTraversal(lpCamera,dwFrame,lpdwNodes);
      }

    itChild++;
    }

  // traverse visitors

  setNodeIterator itVisitor = m_setVisitors.begin();

  while(itVisitor != m_setVisitors.end())
    {
    CGraphNode* lpVisitor = *itVisitor;
    CBVbase*    lpBVNode  = lpVisitor->lpGetBoundingVol();
    CMat4x4     m4Node2World;

    if(lpBVNode)
      {
      if(lpVisitor->boGetWorldMatrix(&m4Node2World))
        lpBVNode->vSetTrf2World(&m4Node2World);
      }

    lpVisitor->vTraversal(lpCamera,dwFrame,lpdwNodes);
    itVisitor++;
    }
  }

/**********************************************************************************************************************/
/*                                                OVERRIDABLES                                                        */
/**********************************************************************************************************************/

/************************************************ hrDraw **************************************************************/
// draw all objects in node                                                                                             
// 28/04/00, M - 05/10/00 visibility test                                                                               
// in : current camera                                                                                                  
// out: _OK_ or error ID                                                                                                
/**********************************************************************************************************************/

HRESULT CGraphNode::hrDraw(const CCamera* lpCamera)
  {
  if(!lpCamera) return _ERR_(_GLOBERR_BADPARAM_);
  CCamera*   lpCam    = const_cast<CCamera*>(lpCamera);
  CBVPlanes* lpPlanes = lpCam->lpGetBVPlanes();

  // objects

  listObjIterator itObj = m_listObjects.begin();
  if(itObj != m_listObjects.end())
    {
    vUpdateBaseLights();                                    // update node's list of lights
    m_lpRenderer->boUpdateLights(this);                     // enable/disable renderer lights
    }

  while(itObj != m_listObjects.end())
    {
    CGraphObj* lpObj  = *itObj;
    bool       boDraw = true;
    bool       boAddV = false;

    if(lpObj->boIsVisitor())
      {
      if(lpCam->boAlreadyDrawn(lpObj)) boDraw = false;
      else                             boAddV = true;
      }

    boDraw &= lpObj->boIsVisible();

    if(boDraw)
      {
      CMat4x4  m4Obj2World;
      CBVbase* lpBV = lpObj->lpGetBoundingVol();
      if(lpBV && boGetWorldMatrix(&m4Obj2World))
        lpBV->vSetTrf2World(&m4Obj2World);

      if(lpCam->dwIsInFrustum(lpObj))
        {
        lpObj->vSetCurrentCamera(lpCamera);
        if(!lpBV || (lpPlanes->hrIntersection(lpBV) != CBVbase::_OUTSIDE_))
          {
          lpObj->hrDraw();
          if(boAddV) lpCam->boAddVisitor(lpObj);            // only when it's really drawn !
          }
        if(lpBV) lpBV->hrDraw(this);
        }
      }

    itObj++;
    }

  // node's BV

  CBVbase* lpBV = lpGetBoundingVol();
  if(lpBV) lpBV->hrDraw(this);
  return _ERR_(_OK_);
  }